Site Art - pi, e & phi
'Maths Made Elementary' Logo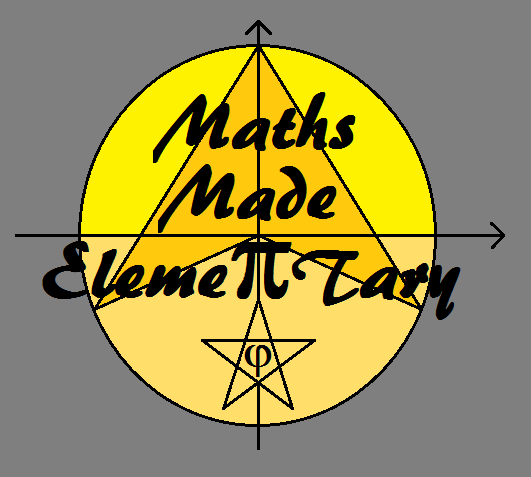
Ok, so I admit the above logo is not exactly the best work of art you'll ever see, but hopefully the geometrical reminders contained within my emblem will make up for the lack of aesthetic appeal and prove pleasing to the intellect if not pleasing on the eye.
I've basically attempted to bring you the rarity of a logo intended to educate, empower and potentially raise your next test result as opposed to achieving those all-too-common, ulterior, marketing goals. If you will, think of it as my small protest against the capitalist model with its logos and advertising designed to do the exact converse - to hypnotise, disempower, and part you from your cash; to empty minds before emptying wallets.
As I'm sure my students will be able to attest, my logo depicts a circle centred on the origin, or point (0,0), whose equation is given by:
x2 + y2 = r2
with r representing the radius of the circle and ±r the values for both pairs of x and y-intercepts.
The orange shape at the centre is called a concave quadrilateral and is made up, in this case, of a pair of congruent, isosceles triangles (assuming I managed to draw my background shapes as intended with a vertical line of symmetry through the centre).
j (pronounced phi), π and the pentagram (5-pointed star) feature prominently in my design also, and I discuss all three in greater detail later in this section including j's relationship to the pentagram.
Finally, I wouldn't be forgiven if I didn't point out that the angle subtended by the arc at the centre is twice the size of the angle subtended by the same arc at the circumference, as per the 'double angle theorem' in circle geometry.
So there you have it. I hope I've proved there's much that can be learnt from even a simple logo when it's been constructed with education in mind. To many more of you I guess the only thing I'll have demonstrated in this exercise is that I seldom leave the house these days.
Now that we've got the amateur stuff out of the way, I should say a few words about the other designs incorporated into the home page of my site.
First up is the ubiquitous π.
π
π is an irrational number. In mathematical terms, this means that π is made up of an infinite, non-recurring, decimal expansion which cannot be expressed as a fraction 'a' over 'b' where 'a' and 'b' are integers. π, like Euler's number e which I discuss later, is not only irrational but also transcendental, or non-algebraic. This means it can never be the 'root' or solution to a non-zero polynomial with rational coefficients.
Most of us first encounter π during secondary level education. It's normally introduced into the school curriculum around year 9 (age 14) and in the context of circles. At perhaps its most fundamental, π defines the ratio between the circumference and diameter of a circle - that most abstract of geometric forms.
I describe a circle here as being an abstraction because nobody has ever actually seen a circle, 'perfect' or otherwise. In fact, the term 'perfect circle' is a bit of a misnomer since any circle at all would possess infinite perfection if it could only be rendered. In other words, there are no degrees of circledom. It would be a bit like describing something as being 'very infinite' as opposed to just 'infinite'. A shape either is or isn't a circle.
We see the futility of all attempts to construct a circle when we consider that an approximation for this abstraction is simply a many-sided regular polygon whose closeness in form to that of an idealised circle improves as you add more and more sides. The ancient Greek mathematician, Archimedes, spent much of his time using this polygonal approach to continuously improve upon his own approximations for π. Clearly, you can always add one more side to your regular polygon. It would require an infinite number of infinitely small sides for your polygon to actually qualify as a circle - a holy grail which must therefore remain forever beyond the reach of us mere mortals.
As an aside, the doubt over how many sides a circle possesses is one that often arises. Some maintain none, others one and others still an infinite number of sides. As for myself, I must confess my ignorance as to the correct answer. The problem here is that our conventional wisdom breaks down when we're confronted with zero and infinity. If we say the circle has an infinite number of sides, then a finite circumference divided by an infinite number of sides suggests that the length of each side must be so vanishingly small as to equate with zero. But even a billion sides of length zero will not get me from A to B no matter how small my distance A to B is. So here we see how infinity leads us to zero and thus a logical contradiction. In other words, to have an infinite number of sides, a polygon must have no sides at all. The assertion of one extreme leads us inevitably to conclude its opposite.
The situation appears similar to Zeno's Paradox in which Achilles, having given the tortoise a head start in their race, must forever remain trailing. He simply cannot traverse the infinite number of intervening, albeit lessening, distances between himself and the tortoise so as to completely close the gap which exists between them. Logically, we deduce that the tortoise must always remain ahead, although practically-speaking, we see the absurdity of this deduction.
Where infinity meets zero we encounter the logical absurdity of an irresistible force meeting an immoveable object. When this happens, all bets are off. For a thoroughly enjoyable and fascinating read about our historical struggles with concepts such as zero and infinity - ancient and more contemporary - I recommend Charles Seife's book Zero: The Biography of a Dangerous Idea
The impossibility of a perfect circle gives us some clue as to the impossibility and futility of any attempt to evaluate π precisely, at least to a number of decimal places beyond a finite limit. In the same way that you can only ever obtain improved approximations for a circle, you can only ever improve your approximation of π by evaluating this number to a greater number of decimal places than you did previously. Geometrically speaking, an approximation for π calculated from a regular polygon containing one million sides will be better than a polygon containing only one thousand sides, but obviously not as good as a polygon containing ten billion sides, and so on... I think you get the picture.
I doubt there's anything I've said, or could ever say about this number which hasn't already been said. In fact, given π's irrationality in the mathematical context I described above, everything I have said and everything I am about to say is already contained somewhere within the infinity of this number's unending decimal expansion. It would only require that you decide on a cipher code to use before setting out on your journey to uncover these words, although why anyone would want to uncover anything I said, specifically, is beyond me! After all, It's not for nothing that I go by the nom de plume, 'melluvahess', on my blog. (In most cases I tend to rely on the statistical inevitability that if I generate sentences of words for long enough I might accidentally write or say something remotely interesting or meaningful by virtue of sheer chance alone. So please persevere!)
Let us delve deeper into a hypothetical investigation of this infinite string of numbers which follows the decimal point in π. A property to note is that you will have no way of predicting any one number you encounter in π's sequence from the numbers which preceded. This unpredictable nature of π arises from its property of mathematical irrationality. To uncover strings of numbers within π's decimal expansion which possess any perceptible meaning, albeit accidental, a simple base-26 alphabetical cryptogram cipher will serve just as well as any. Better still, let us adopt a mode-26 approach to strings of 2-digit numbers with the numbers "01" representing the letter "A", 02 - B, 03 - C, and so on all the way up to 26 for Z. Then, if we want, we can have 27 cycle back to the letter "A" the way that 13 cycles back to 1 on a mode-12 clock face.
Once you've armed yourself with a suitable cipher decoder, the next thing I would advise is that you allow yourself plenty of time before you embark on your journey through π - ideally an infinite amount of time as it may be a while before you encounter anything of substance, or anything at all resembling more than the 'mell of a hess' I referred to earlier. But seriously, time is a big factor here so you may want to pick a week where you don't have quite as much on. If you need an excuse for skipping work, predestination is always a good one... "Your non-attendance at work was written in the numbers long before you ever set out to investigate those very same numbers." Just hope your boss doesn't think too long and hard about your excuse and counter it with the fact that every single alternative was also written in those numbers including those alternatives in which you actually turned up to work. Don't worry too much about this potential rejoinder, however. He's a boss and, as such, is bound not to be thinking long and hard about anything. After all, it's your job to think long and hard about things, not his.
I must also warn you about one very strange thing that inevitably happens on this road to infinity when you've travelled it long enough. Sooner or later you start encountering long passages that not only describe in extraordinary detail what you, personally, have done - or are going to do - in your life, but also what you're doing right at the exact moment you stumble across these passages. It can be very off-putting, especially when your very next move and reaction is being read back to you in the numbers as you decipher them. You start feeling disconcertingly like a character in a script, except one who has suddenly woken up to the fact that his whole life is following that same script. A popular verse from Shakespeare's play, 'As You Like It', springs to mind:
All the world's a stage,
And all the men and women merely players.
They have their exits and their entrances;
And one man in his time plays many parts…
Speaking of which, you will sooner or later come across this exact same verse on your journey through π. In fact, Shakespeare's entire back catalogue of works can be found in π if you search long enough. So much for free will! I used to think ol' Bill actually had talent until I started giving this whole concept of predestination some deeper thought. In actual fact, all he seems to have done is find a way to reach far enough into π and pull out some old pre-written text. Text written into π at the inception of our universe approximately 13.72 billion years ago no less, so you can add 'dated' to my assessment of Shakespeare. Still, although plagiarised from π, his plays are something to look forward to and certainly a welcome break from some of the more disconcerting and meta-fictional aspects of narrative you're bound to come across on your trip. The only problem with the plays is that you'll have to read through countless unfinished editions before you eventually come to one which is complete. I hope fans of Shakespeare will permit me just a little bit more irreverence here when I dare to speculate you may even encounter many improved versions of these plays including a version of Hamlet in which the body count is not quite so gratuitously high!
You will find all of Man's greatest literature embedded in π including those works he most reveres. That most holy of books representing God's unalterable word, the Bible, is in π's unending decimal expansion, including countless altered versions! Even the uncensored version can be found in π. I refer of course to the unbowdlerised edition which wasn't expunged of the objectionable text which would otherwise have rendered it less palatable for mass consumption.
Actually, it's quite tempting to fall to your knees and genuflect in worshipful deference when you first uncover the irrational words of the Bible in this rational number. Excuse me, I see that I have worded that last sentence precisely the wrong way around. How embarrassing given that my 'delete' function is temporarily out of order. I meant of course to say 'the rational words of the Bible in this irrational number'. Anyway, to counter your more primitive instincts here, it's important to remember that within the infinity of π, all things, no matter how vastly improbable, are almost certainly inevitable. I must emphasise this reminder because I'm aware of how easy it is for our misplaced intuitions to erroneously interpret these 'small probability events' as evidence for a conscious designer at work. It's especially sobering when you cast your mind back far enough to earlier trips through π and remind yourself that you encountered countless word-for-word renditions of Hitler's fanatical 'Mein Kampf' long before you came close to a perfect rendering of that paradigm of reason, tolerance and moderation - the Bible. It makes you wonder where the priorities of such a hypothetical, benevolent and humanitarian agent could reside exactly.
I think I'll abandon for now any more surreal adventures through π and allow you to imagine for yourselves the endless rabbit holes which await you there. Suffice to say, an infinity of possibilities awaits those brave enough to embark.
It would seem I've taken a wildly meandering and exaggerated metaphysical detour away from what started out as an attempt to summarise this well-known number. I suppose I have proven once again that I should never be allowed anywhere near a keyboard and internet connection. Rest assured though, the information you read on Wikipedia pertaining to π will strike you as being far more reliable, sensible, coherent and not quite as discursive as my own. Well, I assume it will be. I self-evidently haven't checked it out myself yet.
To those of you who have persevered this far, I can only admire your superhuman levels of tolerance. You're certainly ready for the trip through π of which I speak. And for those of you looking for something less rambling and more illuminating on the subject of π, I would have to recommend Petr Beckmann's book, A History of Pi.Here you will get to read about this fascinating and enigmatic number in its full historical and academic context, and in stark contrast to the surreal context I've attempted to expound.
Leonhard Euler (1707 - 1783)
Leonhard Euler was an eighteenth century Swiss mathematician. He is widely regarded as one of the greatest mathematicians of all time. How appropriate then that the equation widely considered the most remarkable and beautiful of all time should have been discovered by Euler.
The equation in question has become known as Euler's Identity and neatly and concisely relates no less than five fundamental constants to each other including Euler's own number, e.
Euler's Identity is most commonly expressed as follows:
eip + 1 = 0 (Euler's Identity)
This identity is just a special case of Euler's own formula
eiϴ = cosϴ + i sinϴ (Euler's Formula)
but with π replacing ϴ.
If you'd like to use Euler's Formula to try deriving Euler's Identity for yourself, then remember to evaluate your angles in radians. Tip: Since π radians is equivalent to 180°, it follows that
cos π = -1 and sin π = 0.
Now let us take a closer a look at one or two of the 'famous five' fundamental constants which some of you may not be quite as familiar with:
Like π, e is an irrational and transcendental number which occurs frequently in nature. Its approximate value is 2.71828 and its decimal expansion is infinite and unrepeating just like that of π.
The credit for this number's discovery goes to the seventeenth century mathematician, Jacob Bernoulli, who stumbled across it in the latter half of the century before Euler's birth. Bernoulli made his discovery whilst analysing a problem on continuous compound interest in which the following limiting expression is found to tend to e as the number, n, tends to infinity:![]()
The number, e, was first popularised by Euler as a natural base for logarithms. Although Euler did not discover the existence of this naturally occurring constant, the number takes its name from this great mathematician all the same due to the extensive work and major concepts that Euler developed around it. It was also Euler who developed the concept of power series expansions including one for his very own beloved number, which I have outlined below:![]()
Next up is the imaginary number, i, which as its name suggests, is one of the more bizarre, abstract and difficult numbers to attempt to conceptualise. Imaginary numbers are introduced to deal with negative square roots not permitted by conventional mathematics. To bridge the gap between real and non-real numbers, it was thought necessary to first define a number, 'i' equal to √(-1) and to call it 'imaginary' by virtue of it being evidently a 'non-real' abstraction of sorts.
Despite its imaginary nature, 'i' has a number of practical applications such as the calculations it facilitates in the half-real, half-imaginary complex plane. The complex plane is like Descartes' 2-dimensional Cartesian x-y plane with its 'real' horizontal x-axis, but with the novel feature of an 'imaginary' vertical axis replacing the standard y-axis.
Strangely enough, despite the difficulties we have conceptualising imaginary numbers, they prove invaluable in real-life applications including calculations utilised by modern-day radar systems in guiding planes safely through aerospace.
I suppose the greatest mystery surrounding 'imaginary' numbers is that they can have any 'real-life' applications at all. Out of the pure abstraction of an imaginary axis, or dimension of space, we can derive actual uses for this imaginary realm in the real world we inhabit. It's as if this plane, forever beyond our capabilities to view directly, is nevertheless casting a perceptible shadow on to our own real world. I sometimes wonder if our imaginary counterparts have a radar technology of their own with which they conversely resort to computations with 'real' numbers in order to operate their devices!
As I'm sure you will agree, I cut you a rather large slice of π earlier, so assuming there's only so much π even the most ravenous appetites can stomach, I will skip over any further digressions into this number. Should you ever regain your appetite however, I can thoroughly recommend Petr Beckmann's book, A History of Pi.
As for the two remaining and more familiar numbers of 1 and 0, I will not go into any detail here. Suffice to say, the number 1 can be considered the building blocks of all other numbers and you can read more about 0 in Charles Seife's excellent book, Zero: The Biography of a Dangerous Idea, which I mentioned earlier, and which gives a dramatic and intriguing account of mankind's struggle to come to terms with this most enigmatic of numbers.
Although blind for the last seventeen years of his life, Euler kept up his prolific and unparalleled output demonstrating that, despite his blindness, he could still see further and keener than most.
I will leave the final word on Euler to a contemporary of his - a mathematician whose own greatness should leave us in no doubt as to the incomparable genius of Euler:
"Read Euler, he is our master in all" ..... Pierre-Simon Laplace (1749 - 1827)
The Golden Ratio, j 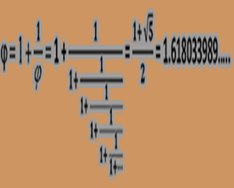
The golden ratio is denoted by the Greek letter, j (pronounced phi), and, as with both the numbers π and e, which we looked at previously, is irrational. Unlike these numbers, however, j is not transcendental since you can actually derive this number as a root of a non-zero polynomial with rational coefficients. Furthermore, such a solution is demonstrated explicitly in surd form as you might be able to make out from the admittedly blurry image above. I have rewritten this evaluation for j below:
j = (1+ √5)/2
So why have I tried to pass off equations written on a coloured background as art? Well, I'm hoping that having considered Euler's Identity from the previous section, you may now be convinced that there can exist a majesty and a genuine aesthetic appeal in a mathematical equation the equal of anything you will see exhibited
in any other art form. Moreover, I think the various depictions of j illustrated above are, in essence, one such example. Perhaps this is an opportune moment to quote one of my favourite twentieth-century mathematicians and philosophers on the subject of mathematical aesthetics:
"The true spirit of delight, the exaltation, the sense of being more than Man, which is the touchstone of the highest excellence, is to be found in mathematics as surely as in poetry"..... Bertrand Russell
At the centre of my image is an infinite series of nested fractions known as an infinite continued fraction. This feature of j derives from its irrationality, but can also be seen to derive from the self-referential and recursive nature of the equation to the left of the continued fraction. This recursive equation reveals something quite telling about j: It just so happens that j has the unique property of being exactly 1 greater than its own reciprocal. In other words
j = 1 + (1/j). A corollary of the self-referencing contained within j is that this equation can also be re-written as j = 1 + (1/(1 + (1/j))) and continued on forever as better illustrated in the image above.
This mathematical depiction of j's property of infinite recursion also offers us useful insight into the fractal nature of those naturally existing forms and geometric abstractions with proportions either equal to, or exhibiting convergence to, j's value 1.618033989....
By fractal here, I mean 'looking the same', or 'exhibiting self-similarity', at all possible scales. Look again at the continued fraction above and imagine the fraction continuing on forever down the page. Now if you zoom in and take a snapshot of any portion of this fraction, you'll find that you have no sign posts or reference points to tell you how far down the page or how far into this recursive fraction you've actually gone. Moreover, it really makes no difference how far you've zoomed into these Mandelbrot-type fractals - numerical or geometric - since their forms can be extended infinitely in both directions without any change to their structure - upwards and downwards or inwards and outwards. (Faced with such inescapable concepts of relativity, Blake's grain of sand qualifies every bit a world as our own world a grain of sand. And for that matter, all our professed troubles as great or as small as we choose to perceive them.)
The naturally realised equivalent to the golden ratio's infinitely continued fraction effect is nicely demonstrated in the logarithmic spirals of a nautilus mollusk as shown in the picture below. These spirals extend outwards in proportions very close to that of j. This is more than just coincidence. Nature - specifically the process of natural selection - unconsciously but very much non-randomly, converges upon this number as a way of optimising the growth of various organisms which have the same dilemmas as all living organisms, namely, how to optimise growth when constrained by limited space and resources.
The logarithmic spirals of a nautilus mollusk
The same fidelity to the golden ratio can be seen at work in the branching ratios of trees. It just so happens that those trees whose branches divide and sub-divide in ratios close to that of the golden ratio, manage to maximise their overall foliage coverage and surface area exposure to the sun's life-giving rays. This then optimises the amount of energy a tree can take in thus giving it every chance of surviving long enough to pass its genes on to the next generation. There is no conscious deliberation on the part of the tree to remain faithful to the golden ratio. The tree chose neither its genes nor its branching strategy; it's just fortunate enough to have a pre-ordained strategy which exhibits branching in conformity to this number of optimal proportion, j, thus standing it the best chance of surviving long enough to make further j-branching copies of itself into the next generation. There would have been many more species of trees which did not obey golden ratio branching strategies. However, we don't see as many of these trees around today because they died out; they were non-optimal. This is natural selection in a nut shell... literally. If I was to use one word to describe the process of natural selection it would be 'death'. Nothing personal, 'just death'... Optimalistically enough!
As with the algebraic, continued fraction depiction of j in our original image, you can again see the self-similarity, 'worlds-within-worlds' theme played out in both the tree-branching fractals and the nautilus. In the case of the nautilus, no matter how much you magnify, or 'zoom into', the centre of this image, you have no way of discerning what magnification factor you used by reference to these infinitely repeating structures unfolding before you, nor any way of knowing how far in you actually are. The same applies to fractal trees. You have no way of knowing how large or small you are, or indeed which branch you happen to be residing on relative to the whole tree. Of course, in these infinitely recurring geometric abstractions, the concept of a whole tree or 'whole anything' is a meaningless one. Unlike the Russian dolls, there is no largest or smallest start or end point. It's Russian dolls all the way down! And all the way up for that matter!
I have included a design of my own theoretical branching fractals below to show you some more of this golden ratio self-similarity at work, albeit theoretical in the context of my illustration. Hopefully this will give you a feel for how this property of golden-ratio-proportionality scaling relates to trees in the real world.
Tree Fractal Branching in conformity to j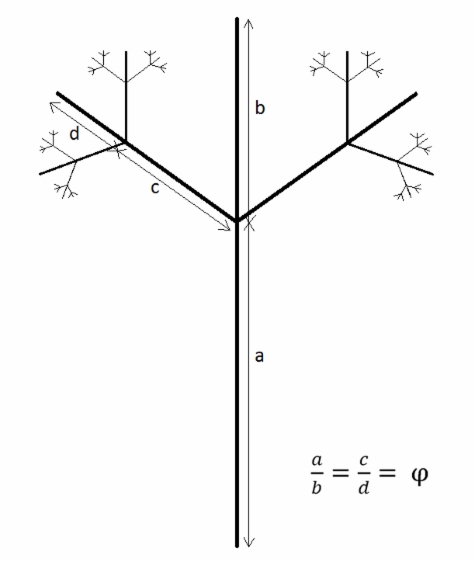
Leonardo Fibonacci (1170 - 1250)
Leonardo Fibonacci was an Italian mathematician, whose efforts to introduce the mathematical methods of the east and middle east would radically change western mathematics as we know it today.
Regarded by some as the most talented mathematician of the Middle Ages, Fibonacci's greatest contribution to the field of mathematics came about with the publication of his 1202 book entitled Liber Abaci or 'Book of Calculation'. In this book, Fibonacci introduced the west to the superior Hindu-Arabic numerals, which would soon supersede the inefficient and cumbersome Roman numerals still in use throughout Europe during his time. This new base-10 number system is the same one we use today with its numbers 0-9 and with its concept of number placement value.
The first known recorded use of these numerals can be traced back approximately two thousand years to India. However, these numerals would later come to be more commonly known as Arabic numerals since it was the Arabs who, around the ninth century, adopted and successfully propagated the methods of the Indian mathematicians throughout their expanding Middle Eastern Empire.
In his book, Liber Abaci, Fibonacci also introduced the West to a number sequence he derived by modelling the population growth of breeding rabbits. The Indians had actually hit upon this sequence centuries before Fibonacci, but as far as is known, Fibonacci was the first to relate the terms of this sequence to a viable model occurring in nature, namely rabbit population growth. As a result, the numbers of this particular sequence have come to be known today as Fibonacci numbers. The reason I mention these particular numbers is due to their close relationship with the golden ratio which I will now attempt to expound.
Fibonacci numbers are generated as terms in a sequence using the following rule:
Starting with the numbers 0 and 1 as the first two terms in a sequence, every successive term is generated as the sum of the two terms which preceded it. So the 3rd term in the sequence is just the sum of the first two terms, which is given by 0 + 1 = 1. The fourth term is then just the sum of the second and third terms and is given by 1 + 1 = 2. Continuing to apply this rule, we can generate as many terms as we care to. I have listed the first eighteen terms below:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597
The interesting bit comes when we start to compare the ratios of adjacent terms in this sequence. What we find is that the further you move along the sequence, the closer the ratio of one term to its succeeding term converges upon the golden ratio. To better clarify this property of golden ratio convergence amongst Fibonacci numbers, I will introduce some fairly basic notation.
Let's take F(n) to be the nth term in the Fibonacci series and F(n+1) to be the (n + 1)th term, i.e. the term which comes after the nth term. Using this particular notation, the beginning terms of the sequence can then be denoted by F(1) = 0, F(2) = 1, F(3) = 1, F(4) = 2, and so on. The interesting property to note here is that as n approaches infinity, the ratio F(n):F(n + 1) approaches 1:j or just j when expressed as a single factor multiplier. This just means that as n gets very large, and we start to reach higher Fibonacci numbers in the series, then F(n + 1) / F(n) converges upon the number j.
So yet again we see the emergence of this golden proportion in nature, this time in a series modelling population growth. To conclude this short chapter on Fibonacci numbers, I have demonstrated the golden ratio convergence of this series of terms in the diagram below: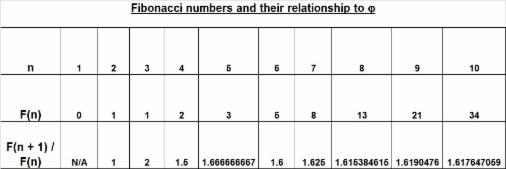
From the table, you can see that by the time you reach the tenth term in the sequence, F(n + 1) / F(n) is just the golden ratio correct to 3 decimal places. Although not shown above, you would find that by the time you reach the 25th term in the sequence, F(n + 1) / F(n) is given by 75,025 / 46,368 which is already j correct to as many as 9 decimal places.
The golden section
We can go back even further in time than Fibonacci to see evidence of Man's burgeoning relationship with this golden number. Unsurprisingly enough, we are led back to ancient Greek civilisation, and to an era so well developed academically, it would take many centuries following the tragic decline of this great culture for the rest of the world to start recovering some of its lost knowledge and brilliance. As Lord Acton once put it,
"Save for the wild force of Nature, nothing moves in this world that is not Greek in its origin."
Being the great mathematicians, philosophers and all-round scholars they were, the ancient Greeks took more than just a passing interest in j and were able to decipher some of its more unique and fascinating properties. This is no doubt how the number came to inherit its Greek letter notation. Their knowledge of this number may have first come about thanks to the Pythagoreans - a number-worshiping cult of mathematicians and philosophers named after their eponymous founder and leader, the famous Pythagoras.
Over 2,500 years ago, the Pythagoreans set themselves the following task: to draw a line of any length and then divide it in such a way that the ratio of the longer segment to the shorter is equal to the ratio of the line as a whole to the longer segment. In other words, to segment a line in such a way that the whole is to the longer segment as the longer segment is to the shorter segment.
For the sake of simplicity, I have arbitrarily assigned the value 1 to the shorter segment and shown you below how this problem translates algebraically to solving a quadratic equation whose solution yields the golden ratio, j. Incidentally, the fact that we can solve a quadratic polynomial for j explicitly in this way is the reason why j does not qualify as 'transcendental'.
The golden ratio derived from Pythagorean line segments
Now to examine a regular 5-sided pentagon's relationship to the golden ratio:
The golden ratio and the pentagon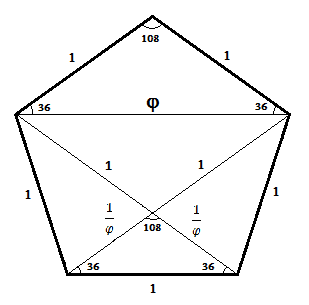
Using the cosine rule, we can prove that the diagonals of any regular pentagon with sides of length 1 are just j in length (as depicted in the diagram above). Assuming the angles shown are already self-evident to readers familiar with theorems which describe angles within n-sided regular polygons as well as angles within isosceles triangles, then rearrangement of the 'cosine rule' formula to determine the base length of the uppermost triangle in our pentagon will yield a way to determine the length of these pentagonal diagonals as follows: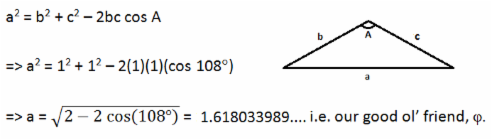
Using the same afore-mentioned angle theorems, we can also show that the angles within the lowermost triangle are 36°, 36° and 108°, thus matching the angles in the top triangle. This is enough information to show that both these triangles are mathematically similar meaning that the ratios between corresponding sides in both triangles are equal. We can use this fact to determine the length of the top adjacent sides, or 'legs', of the smaller isosceles triangle sitting at the base of the pentagon. We can label each side 'x' as both sides are necessarily equal in length being the legs of an isosceles triangle. We can then solve for 'x' by using an equation which exploits the mathematical similarity we know exists between the top and bottom triangles. This gives us the following solution: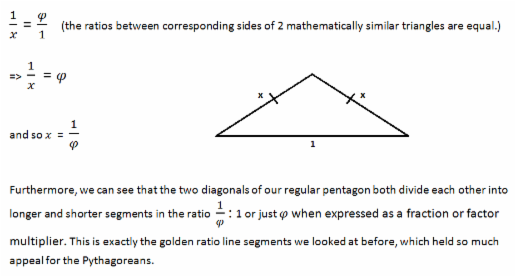
The golden ratio and the pentagram
The pentagram is the shape you're left with when you remove the outer edges of a pentagonal network of connections. Doing so leaves you with just five lines which connect every vertex from the original pentagon to every other non-adjacent vertex to form the five-pointed star. The pentagram's own conspicuous relationship with the golden ratio should come as little surprise to us when we consider that this shape is simply the offspring of the regular pentagon whose own proportions are written large with the signature of this number.
I have demonstrated some of the numerous manifestations of j in my diagram of a pentagram below:
The repeated occurrence of the golden ratio in the pentagon - and in particular its derivative, the five-pointed star or pentagram - is largely why these figures became symbols of worship for the Pythagoreans. So enchanted were they by this number, j, they took it to be a divinely sanctioned proportion.
Finally, I couldn't resist the opportunity to show you how the pentagon and pentagram can be merged together to create a recursive fractal design which appears the same at all scales regardless of how far you zoom in or out of the centre of this image. To those interested, I was able to construct this fractal pattern in a very straightforward manner using tools within 'Paint'. The special properties of our special little number make it possible to perfectly inscribe a pentagram within a pentagon within a pentagram within a pentagon within a pentagram within a pentagon, and so on, ad infinitum. Who said you can't have fun with straight lines?
Pentagrams within pentagons within pentagrams.....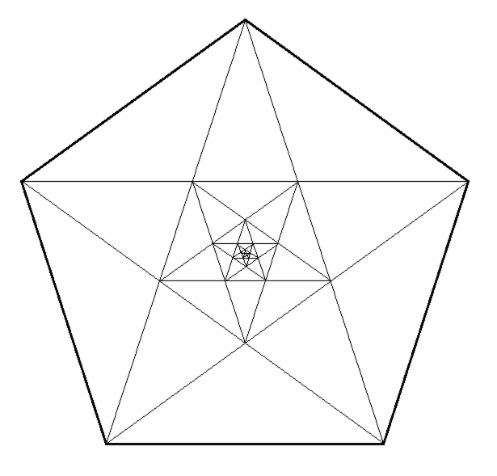
The types of symmetries and fractals you see displayed in the illustrations above are in large part the reason why the number 1.618033989... has earned itself so many different nicknames and applications throughout history. Sometimes referred to as the golden mean, the golden section, the divine proportion, the number of perfect symmetry and even the number of perfect beauty, this number's man-made uses have been found in art and design, architecture, music and the modern-day manufacture of various objects such as furniture items and television sets. These modern-day applications are attempts to incorporate so-called 'golden rectangles' so as to create, disputably, the most visually pleasing effect on our hard-wired senses.
For those of you interested in further reading, I can recommend Mario Livio's book, The Golden Ratio: The Story of Phi, the Extraordinary Number of Nature, Art and Beauty.
And for those of you who have persevered with me up to this point, I have this advice: Strap yourselves in as happy hour at Pete & Bernie's Philosophical Steak House is about to get underway!..... again.
Phi of the beholder, natural selection and quantum observations
Could it be possible that 'beauty' amounts to no more than the degree to which the proportions of an object conform to ratios of symmetry, be they the 1:1 of a perfect square, the 1:j of a golden rectangle, or some other ratio?
For me, the question is potentially unanswerable as it calls for an explanation which assumes the existence of the very thing we're trying to explain. In addition, it begs the more pertinent question, "What is beauty?" Whichever way you look at it, an answer to this question will invoke an opinion or value judgement. It becomes impossible to make a determination which removes 'mind' from the equation. Being mind-dependent, it therefore evades any definition which could be considered objective or even the smallest bit meaningful at a fundamental level. Perhaps moments within Tchaikovsky's Sixth come close, but that's about as much as I'll concede!
We may be able to make further inroads in our analysis by replacing the word 'beauty' with the word 'utility' or the word 'beautiful' with the word 'useful'. We need look no further than the theory of natural selection to see this idea made plausible; maybe even justified a priori.
For example, it's a useful thing if a male chimpanzee finds a female chimpanzee attractive. A concept of beauty, no matter how illusory, will serve the male very well in facilitating 'mate selection' criteria, thereby offering a useful strategy by which the male can get copies of its genes into the next generation. Inevitably, these strategies will be refined and adapted over a long period of time to enable discrimination between one female and another. It will no longer suffice to select 'any old vehicle' for transporting its genes into the next generation. Instincts will be honed to differentiate between those mates it considers a good match and those it considers less so. What's more, the chimp needs no conscious awareness of the underlying mechanisms driving its behaviour in order to be able to behave in this way.
It's also a useful thing if chimpanzees find their offspring visually pleasing. Let's consider the alternative: A chimpanzee repulsed by the sight of its young would find it extremely difficult to summon the feelings of charity and sympathy needed to responsibly protect and raise its newborns to reproductive age. This in turn would seriously jeopardise, not only the infant's survival, but just as importantly, the perpetuation of a large proportion of the parent chimp's own genes. After all, the parent has a large amount of genetic material invested in its young. Genes conferring the opposite of an aesthetic affinity for newborn progeny are not the best ones for encouraging responsible, stay-at-home, mothers and fathers. They promote high infant mortality rates and, eventually, lead to the extinction of the same genes which conferred these characteristics. We see less of these genes around today for this reason. Finding babies repulsive is simply not conducive to the continued survival of a species. Finding a baby's features visually congenial is.
Mother Nature in her infinite wisdom engineers the circumstances needed by introducing rules of attraction, at least when she's given sufficient time and enough goes at getting it wrong first of course. It's useful to remind ourselves that during this ongoing process of trial and error that we call 'evolution', approximately 99% of species that ever lived went extinct. That's almost 100%! So much then for 'infinite wisdom' or 'intelligent design'.
All that's needed for evolution in the context of life is organic replicators capable of making copies of themselves which allow for occasional errors, or variations, and which are subsequently subjected to selective pressures within their environment. The genetic copying errors arise randomly, but the selective pressures are anything but random.
For Mother Nature's part, none of the 'selecting' that goes on is intelligent in the way we associate with conscious beings that make preemptive choices. This is where an inversion of reason is required. The word 'selection' for many invokes conscious deliberation on the part of sentient beings. This may be where some people struggle to accept a notion of Nature acting as a selective agent in a non-random way whilst remaining very much unthinking during the entire process. It may be useful here to think of Nature acting as a sort of filtration system for genes; a sort of gene sieve. The everyday sieve we're familiar with is able to filter small debris from large without any conscious choices driving this process. Effectively, the sieve chooses small from large without any intelligent purpose whatsoever. Genes face the same kind of filtration systems but with the emphasis being, not on size, but on a series of tests to check these genes' suitability to an ever-changing environment.
Perhaps we need a further inversion of reason to overcome any lingering difficulties we may have perceiving this notion of 'non-conscious choice'. It might be more accurate to describe Nature as being non-selective rather than selective. After all, it's due to the indifference of Nature that poorly adapted genes eventually perish and better adapted ones prevail. It is because Nature does not intervene on the part of weaker genes that these genes die out. So the process of 'not choosing' and 'not taking sides' ends up creating the deceptive appearance of sides being taken.
Nature does not sit in conscious judgement. There is nothing inherently superior about those genes better adapted to their environment which in any way endears them to some imaginary notion of a judgemental and superintending Nature. We're better off thinking that Nature looks the other way when it comes to choosing between well-adapted and poorly-adapted genes. The truth however is that nature is not in any sense mindfully looking upon things in any given way, favourable or otherwise. Genes well-adapted for surviving survive because they are well-adapted for surviving. For me, the tautology is worth stating.
To try and highlight the fallacy of assigning design, purpose or teleology to nature, we could just as easily infer that Nature desires every living thing to go extinct. (At 99% and counting, it's doing a pretty good job of it after all!) Let's propose then that all of nature is an intolerable battlefield - red in tooth and claw - in which the name of the game is to die out as quickly as possible so as to get away from the unbearable cruelty of it all. When viewed in this way, genes built for longevity are far from optimal. Moreover, they're poorly adapted for accomplishing the goal of extinction. With this new take on matters, it would become as meaningful to say that Nature looks favourably upon poorly adapted genes by helping them to die out more quickly. The truth is that Nature inanimate cares not whether things live or die.
Nature's indifference is simply a consequence of it being completely void of mindful intelligence. In the theory of evolution we see how an unthinking agent can 'select' by 'not selecting' and so effectively do the same job as a conscious entity picking out good from bad. It is this process which creates the deceptive appearance of an intelligent designer at work. Nature is competent, but it's not comprehending. Nature is able to 'select' genes for optimality without ever being conscious of its selection criteria and without having any specific end goal in mind. It's then left to a combination of trial and error and adequate time to accomplish the task of evolving the diverse, well-adapted and complex life forms we see around us today.
In the examples I outlined above, I chose to use chimpanzees to support my ideas for a naturalistic, utilitarian and subjective version of aesthetics. This may strike some as a thinly veiled disguise for deconstructing those things held dear amongst our own species; a half-hearted attempt at being slightly less provocative than I could have been had I used the human species in my examples. I'll probably be undoing any diplomacy on my part by pointing out our own well-known and proven close proximity to the chimpanzee in the phylogenetic 'tree of life'. In fact, we need only go back 5-6 million years to locate a common ancestor between Man and chimpanzee - a period of time relatively brief in evolutionary terms. Furthermore, the genetic drift between Man and chimpanzee over this period has not been nearly as marked or as drastic as some would feel comfortable thinking it's been.
Genetically speaking, chimpanzees are our closest cousins. If chimpanzees are the fourth ape, then we're very much the fifth. It comes as no surprise then to find that we share a huge amount in common with our fellow primates underneath the veneer of our own apparent, higher, cognitive faculties. For those who find such comparisons less-than-flattering, or even provocative, I will seek refuge here by blaming the ape in me for stooping so low as to draw such comparisons. In any case, I often wonder if our close kinship with chimps is an honour which belongs more to us than it does to them!
The father of evolutionary theory himself, Charles Darwin, had this to say by way of reminder:
"We must, however, acknowledge as it seems to me, that a man with all his noble qualities... still bears in his bodily frame the indelible stamp of his lowly origin."
Upon reading this, some of you may be more inclined to agree with the American comic, Steven Wright's, own theory of evolution that "Darwin was adopted!"
All of us living today find ourselves at the end of an extremely long and unbroken chain of ancestors, all of whom were successful in achieving the evolutionary payoff in any strategy which makes an attempt at the closest thing we have to immortality, namely, producing partial replicas of ourselves which stand a good chance of surviving for many generations to come. It is little wonder then that we have inherited those very same instincts. We are led to a sort of anthropic principle of aesthetics:
We find ourselves hard-wired to behold outward appearances in a certain way because our very existence, which enables us to do the beholding, is itself predicated on the fact that our ancestors before us beheld these forms in just that particular way. Had they not, we wouldn't be around now to even ask the question,
"Why do I behold as I behold?"
In evolutionary terms, beauty is revealed for what it is - utility in disguise. We form opinions about what constitutes high aesthetic value and what doesn't based on a whole host of underlying, primitive instincts which motivate these opinions. Our instincts are concerned only with what use is suggested by an outward appearance. When, in hindsight, no obvious use can be found beneath an appealing outward appearance, this is symptomatic only of the susceptibility of our own senses. Our senses can easily be deceived into finding aesthetic value in a form with no obvious use when it resembles a form which does have use. Needless to say, this susceptibility is exploited by much of the advertising which goes on in the world today.
There is no objective source for aesthetics. No matter which way you slice it, you cannot arrive at a judgement as to the aesthetic value of a thing independent of an observer who forms the opinion. Even if a consensus is reached at the level of an entire species, we've added nothing to the claim that these forms can exist independently. On the contrary, we've simply scaled up subjectivity from the individual to the mass.
"The fact that an opinion has been widely held is no evidence whatever that it is not utterly absurd; indeed in view of the silliness of the majority of mankind, a widespread belief is more likely to be foolish than sensible."... Bertrand Russell
The 'beauty' of an object owes its status as much to my assigning it the label 'beautiful' as it does any particular form it may take. If I describe a Turner seascape as beautiful, what I'm actually doing is confessing my own appreciation for how I managed to take the painting's shapes and colours and work them into something I found pleasing in my own mind's eye. I don't wish to detract from Turner, but it was me that did that! My mind gave Turner's art permission to call itself beautiful. This judgement was projected from within; the source for it is not to be found residing intrinsically in the world around me. The fact that a slug no doubt has a different concept of beauty than I do, presuming it finds certain other members of its species attractive, should make it self-evident that attractiveness is as much projection of information on to a form than assimilation from.
But why stop at beauty? We can apply the same reasoning to any adjective we care to choose. Credit (or discredit) belongs as much to the one who perceives a given characteristic in an object (good or bad) as much as it belongs to the object whose form is being perceived as such. Even if these perceptions are warranted by instincts alone, and entirely non-voluntary, they are still imparted from subject to object and wholly reliant on the co-existence of the two. To describe a given quality within a given form as being inherent or absolute, and independent of an observer, would be about as coherent and meaningful as trying to describe the sound of a tree falling over in a forest with no-one around to hear it, or a radio signal transmitted through space with no receiver to intercept and unscramble it.
The forms we take in through our eyes rely on light to transmit information about these forms. Light is the carrier of this information. However, when construed as a noun or an adjective, light itself takes on no meaning without there being an eye to perceive it. Light - along with the shapes, forms and colours which arise from light - is a process or an interaction between object and subject; the thing being beheld and the beholder. The observer and the observed are inextricably linked.
This concept becomes more than mere philosophical supposition when viewed at the sub-atomic scale of the quantum world. Here, we encounter phenomena and strange effects unbeknownst to us prior to the quantum revolution at the beginning of the twentieth century. It would seem a particle's 'state' is very much dependent on whether it's being observed or not. The mere act of observing a particle is influencing what it is that we're observing about its behaviour. It's worth dwelling a moment or two on the following inescapable tautology:
To find out how a particle is really behaving when we're not observing it, we must refrain from observing it.
Therein lies the catch-22.
As it turns out, the unobserved sub-atomic particle hedges its bets and remains undecided in its choice of a fixed state. Until observed, it remains in a probabilistic multitude of positions and states - a superposition we refer to as a wave. At the precise moment of observation this wave collapses to a fixed point we describe as a particle. I will not go into any detail here as to how we can overcome the obvious problem of knowing what anything is doing when it's not being observed. Instead, I will simply allude to the fact that in quantum mechanics we can observe the effects of 'non-observation' in a manner of speaking.
The mystery of quantum phenomena reveals how light's ambiguous nature confounded the best scientists throughout history. Is light a particle or a wave? It would seem the true nature of light polarised opinion as effectively as light polarises itself since the very best minds ever to ponder the question of its fundamental nature remained divided for centuries over the answer. The fact is, light is both a particle and a wave - a wave when unobserved and a particle when observed. It would be more accurate to describe light as 'wavicles'.
Austrian physicist Werner Heisenberg, famous for his 'Uncertainty Principle', and Danish physicist, Niels Bohr, famous for his model of atomic structure, were very much the two protagonists of the quantum revolution which led finally to the ground-breaking Copenhagen Interpretation of 1927. This became the interpretation which would inform much of quantum physics to this day.
For a more thorough treatment of these ideas, I invite you to explore the abundant literature, in particular the famous double-slit experiment. This experiment encapsulates the essence of quantum theory. Those not intrigued by this experiment upon first encountering it have probably not fully grasped its mysterious and convention-defying implications.
Quantum theory doesn't just make us question our fundamental perceptions about the nature of reality, but rather it takes those perceptions and turns them upside down. The conventional wisdom is turned completely on its head.
Niels Bohr had this to say:
"Anyone who is not shocked by quantum theory has not understood it."
Perhaps the ancient mystics of the east - with their adherence to non-dualistic concepts and their embrace of notions pertaining to simultaneous singularity and plurality - had it right in their intuitions all along. It's tempting to think so, and interesting to speculate. However, despite my own affinity for eastern philosophy, I must admit that links between quantum theory and mysticism appear tenuous at best. It would be disingenuous of me not to emphasise at this juncture that quantum mechanics states nothing whatsoever which could reasonably be construed as supporting mystical, spiritual or metaphysical claims. Those who use it to support untestable or pseudo-scientific hypotheses are either being deeply disingenuous themselves, or grossly ignorant of the facts. In any case, anyone wanting to add fictional, unsubstantiated and non-falsifiable metaphysical claims to spice up a science already as mind-blowingly wondrous and revelatory as quantum mechanics is clearly overlooking the moral of the quantum story: Nature provides for us a reality much stranger and awe-inspiring than any fiction. The world is its own magic.
I have not done quantum mechanics the smallest degree of justice in my hasty write-up above. To those of you not already familiar with this branch of science, which is so integral to modern technology, I have only attempted to whet your appetite in the hope that you may further explore for yourselves this strange and wonderful world. To those interested, you will find a vast amount of literature available on the subject, both scientific and popularised.
I hope my quantum digressions have provided some physical and scientific basis for the concept of a merger between subject and object; observer and observed. This has been my ultimate goal after all.
Returning to my opening theme on ratios of symmetry, it would seem j and 1 are both good candidates for numbers bestowing proportions with optimal functionality. Beauty, on the other hand, must remain forever stuck in the realm of the wholly subjective. This will relieve some of you, not least me. As a wise person once said,
"Beauty is in the eye of the beholder... But it may be necessary from time to time to give a stupid or misinformed beholder a black eye.".....Miss Piggy (1974 - ?)
To prove her point, Miss Piggy has asked me to set my readers the following challenge:
Spot the difference
Besides the barely significant fact that each image below appears to be the other image rotated through an angle of 180°, can you spot any other differences?
Young beautiful princess or old ugly woman?
Optical illusions
The misleading 'spot the difference' challenge issued above provides me with a nice segue into displaying enlarged images of the optical illusions and impossible objects featured on the home page of my website.
The inspiration for this art draws largely from the twentieth century Dutch artist, M.C. Escher, whose art was itself mathematically inspired to an extent. The first two pictures below are actual re-workings of Escher's 'Relativity' and 'Waterfall'.
Unfortunately, I have not been able to bring you Escher originals, but I hope you will regard the following as worthy substitutes and excellent pictures in their own right. These are stock art images, so I have no idea who their creators are, but for those of you who would like to explore in detail some of Escher's artwork, I recommend Bruno Ernst's excellent book, The Magic Mirror of M.C. Escher (Taschen 25th Anniversary Series).
Escher's 'Relativity' in 3D
Escher's 'Waterfall' in 3D
Impossible architecture
Impossible Water Feature
Back to Home Page
Dedicated to making maths elementary